【Python】回溯递归法一键解决数独谜题

2023-07-08 / 其他 / 65浏览

【Python】回溯递归法一键解决数独谜题

项目的起源是2019年在临时宿舍无聊玩数独时的想法，当时时间不够就搁置了，直到前几天才想起来。实现过程比较简单，唯一的小坑就是在数字识别的方法选择上。本来打算使用神经网络的，但是能找到的模型都是在mnist上训练的，实测下来正确率只有个60~80%左右，我也不想花时间训练和fine tune模型，于是最后使用了模板匹配的方法。最终还是完成了该项目，也算是完成了一项延迟4年的项目。

视频演示：Python回溯递归法一键解决数独谜题

数独的一般规则

数独是一种逻辑谜题，通常由9×9的方格组成，被划分为9个3×3的小方块。目标是在每个方格中填入数字1到9，使得每一行、每一列和每个小方块内的数字都恰好出现一次，且不重复。

数独的基本规则如下：

每个方格只能填入数字1到9中的一个数字。
每一行中的数字必须是唯一的，即同一行中不能有重复的数字。
每一列中的数字必须是唯一的，即同一列中不能有重复的数字。
每个小方块中的数字必须是唯一的，即同一个小方块中不能有重复的数字。

基于这些规则，数独的谜题通常在开始时会提供一些已经填入的数字作为提示，玩家需要根据这些已知的数字，通过逻辑推理和推断，填写其余的空格，直到所有的方格都被填满且符合规则。

获取数独棋盘状态

数独游戏是Steam上的Sudoku Zenkai，进入游戏，选择难度后就会出现以下谜题，在对应位置填入数字就行。

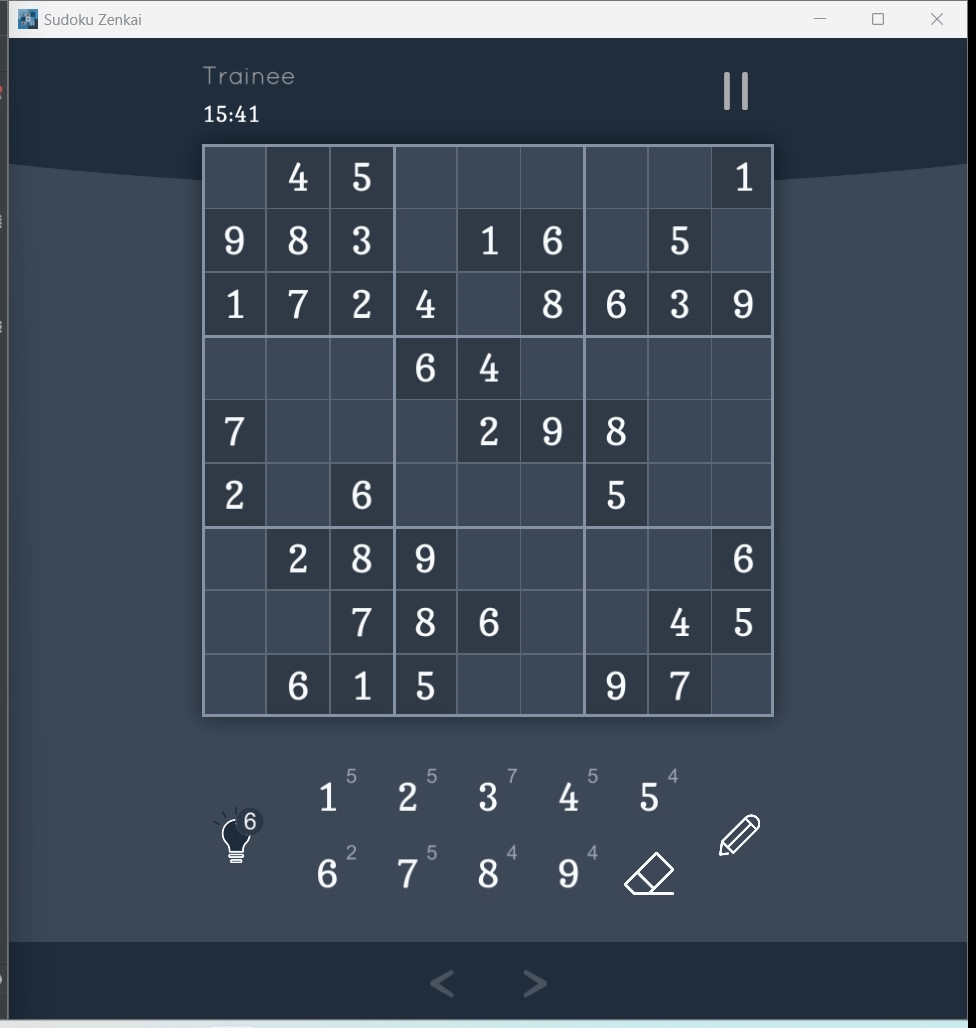
这个截图使用到了pyautogui和PIL库。具体代码如下：

import pyautogui
from PIL import ImageGrab

def get_window(window_name="Sudoku Zenkai"):
    # 获取窗口的位置和大小
    window = pyautogui.getWindowsWithTitle(window_name)[0]

    # 获取窗口的位置和大小
    window_left = window.left
    window_top = window.top
    window_width = window.width
    window_height = window.height

    # 获取指定窗口的图像
    screenshot = ImageGrab.grab((window_left, window_top, window_left + window_width, window_top + window_height))

    # 保存图像
    # screenshot.save("window_screenshot.png")
    # 将PIL图像转换为NumPy数组
    numpy_image = np.array(screenshot)

    # 将NumPy数组转换为OpenCV图像
    opencv_image = cv2.cvtColor(numpy_image, cv2.COLOR_RGB2BGR)

    return opencv_image, (window_left, window_top)

这个函数首先获取指定窗口的位置信息，然后调用grab函数获取对应位置的图像，因此要确保窗口在最上层，这样才可以采集到想要的窗口图像。

随后我们要确定棋盘的位置，也就是这个棋盘的左上角坐标。这一步要用到两个关键函数，filter_color是把图片根据目标颜色过滤，只留下该颜色的像素。get_white_rect函数用来把过滤得到像素做一个统计，获得其中最坐上角的位置。

def filter_color(image, target_color, tolerance=20):
    # 创建一个与图像大小相同的掩码
    mask = np.zeros(image.shape[:2], dtype=np.uint8)

    # 在掩码中将与目标颜色相等的像素置为白色（255）
    mask[(image == target_color).all(axis=2)] = 255

    return mask

def get_white_rect(image):
    top_left = None
    bottom_right = None
    _, binary = cv2.threshold(image, 127, 255, cv2.THRESH_BINARY)

    # 获取非零像素的位置
    white_pixels = cv2.findNonZero(binary)
    if white_pixels is not None:
        # 获取最左上和最右下的白点的位置
        top_left = np.min(white_pixels, axis=0)[0]
        bottom_right = np.max(white_pixels, axis=0)[0]

    return top_left, bottom_right

完整的获取棋盘的函数如下，其作用是把图像形式展示的棋盘（游戏截图）转化成一个9×9的 numpy 数组，进而方便下一步进行递归求解。

def get_sudoku_board(window_img, max_col=9, max_row=9, box_size=64, padding=0):
    # 定义目标颜色
    target_color = (166, 146, 132)  # BGR颜色

    # 过滤图像中的单一颜色
    filtered_image = filter_color(window_img, target_color)
    top_left, bottom_right = get_white_rect(filtered_image)
    core_image = window_img[top_left[1]:bottom_right[1], top_left[0]:bottom_right[0]]
    core_image = cv2.resize(core_image, (572, 572))

    # 坐标
    cord_x = padding
    cord_y = padding
    # 用来剔除分割线的参数
    erode_level = 9

    # 9x9棋盘，每个位置代表对应位置的数字，0为空，即待填数字
    puzzle = np.zeros((max_col, max_col), dtype=np.uint8)

    # 切分棋盘并识别每个位置的数字
    for i in range(max_row):
        cord_x = padding
        for j in range(max_col):
            # 获取对应位置图像并剔除分割线
            box_image = core_image[cord_y:cord_y + box_size, cord_x:cord_x + box_size]
            erode_image = box_image[erode_level:-erode_level, erode_level:-erode_level]
            erode_height, erode_width = erode_image.shape[:2]

            # 调整尺寸 方便识别数字
            square_image = np.zeros((box_size, box_size, 3), dtype=np.uint8)
            x = (box_size - erode_width) // 2
            y = (box_size - erode_height) // 2
            square_image[y:y + erode_height, x:x + erode_width] = erode_image

            # 二值化并识别数字
            _, binary_image = cv2.threshold(square_image, 180, 255, cv2.THRESH_BINARY)
            puzzle[i][j] = get_digit_by_template(binary_image)

            cord_x += box_size + padding
        cord_y += box_size + padding

    print("Difficulty: %d" % (81 - np.count_nonzero(puzzle)))
    return puzzle, top_left, bottom_right[0] - top_left[0]

其中这个双层循环会分割出81个位置的数字图像来，如下所示：

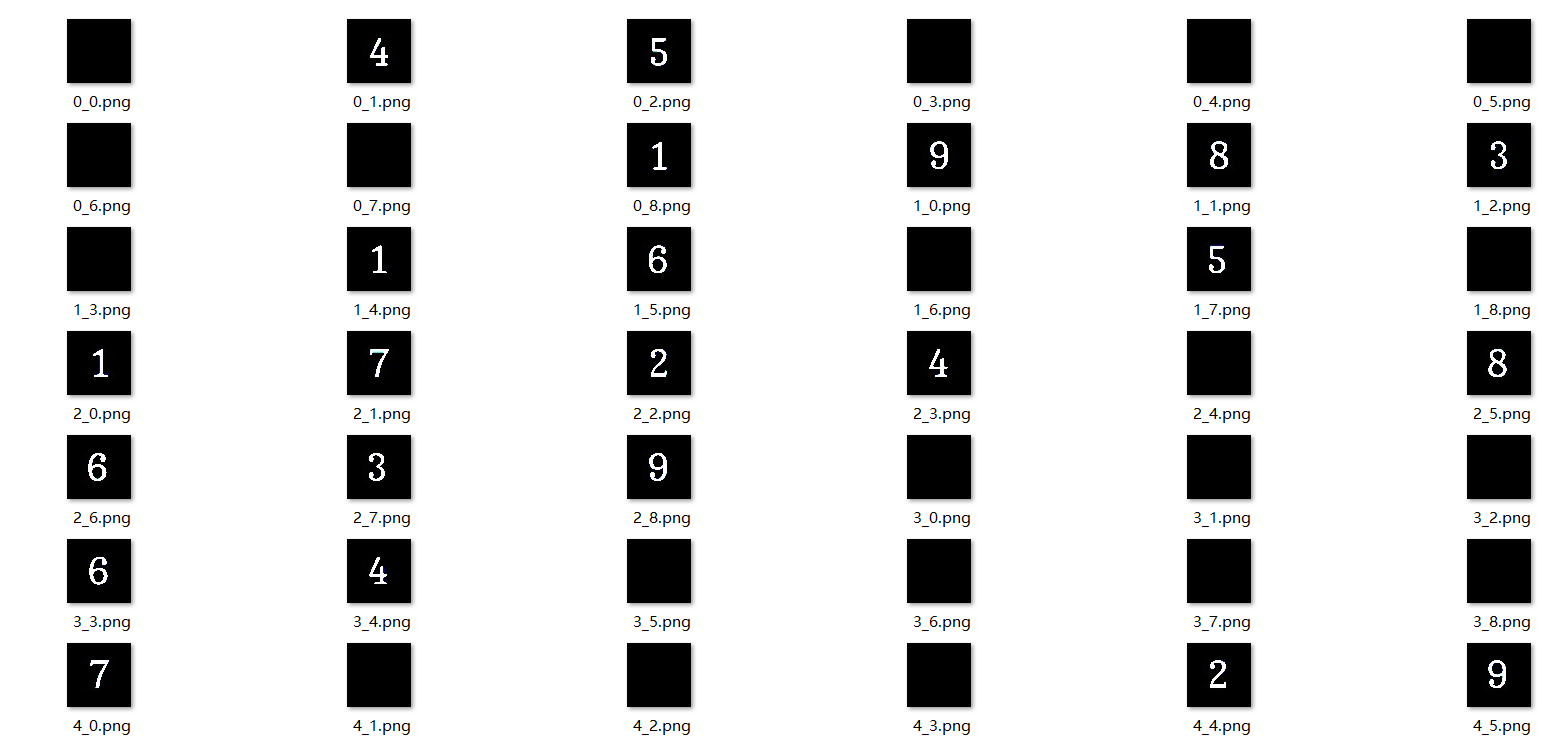
接下要做的就是利用get_digit_by_template函数把每个图片转化成整数类型变量。当然，如果是待填入的数字，那么棋盘上自然为空，对应图像也就是全黑的了。

如前言所说，这里使用基于模板匹配的方法来识别数字。核心代码如下：

def get_digit_by_template(image):
    img_gray = cv.cvtColor(image, cv.COLOR_RGB2GRAY)
    top_left, bottom_right = get_white_rect(img_gray)
    if top_left is None:
        # 如果是全黑的，那么就是零
        return 0

    confidence = np.zeros(9)
    # 读取模板图像和待识别图像
    template_path = 'template/'  
    resized_image = cv2.resize(img_gray, (64, 64))

    # 1到9共9个数字
    for i in range(9):
        image_path = os.path.join(template_path, "%d.png"%(i+1))
        template = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

        result = cv2.matchTemplate(resized_image, template, cv2.TM_CCOEFF_NORMED)
        # 获取最相似的模板编号
        confidence[i] = np.max(result)

    return np.argmax(confidence)+1

模板图片如下：

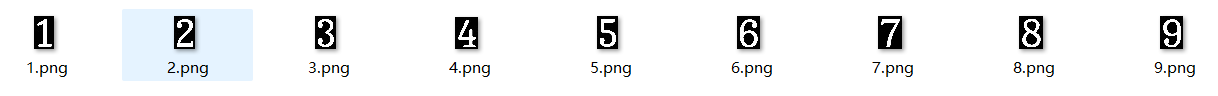
那么到这里就完成了从图片提取棋盘的过程了。

回溯法求解数独

回溯递归法（Backtracking）是一种常用的解决问题的算法策略，它通过尝试各种可能的解决方案，并在发现无法继续前进的情况下回溯（退回）到上一步，重新选择其他的路径继续搜索，直到找到问题的解决方案或者确定无解。

回溯递归法通常适用于在一组候选解的集合中搜索满足特定条件的解决方案。它的基本思想是通过递归函数的不断调用，不断尝试各种可能的选择，并在每一步进行条件判断，以确定是否满足问题的要求。如果当前的选择不符合条件，就回溯到上一步，尝试其他的选择。

回溯递归法的一般步骤如下：

定义递归函数：根据具体的问题定义一个递归函数，确定输入参数和返回值，并编写递归终止条件。
做出选择：在递归函数中，根据问题的要求，做出一个选择，可能是从一组可能的选项中选择一个，或者是在某个范围内选择一个值。
检查条件：对于当前的选择，检查是否满足问题的要求或限制条件。如果满足条件，则继续递归调用；如果不满足条件，则回溯到上一步。
递归调用：在满足条件的情况下，通过递归调用自身，在下一步继续进行选择，进一步探索可能的解决方案。
回溯：如果递归调用返回的结果是失败或无解的情况，回溯到上一步，撤销当前的选择，并尝试其他的选择。
返回结果：在递归函数的终止条件中，返回最终的解决方案或标识无解的结果。

回溯递归法的关键在于不断地进行选择、条件判断和递归调用，通过搜索整个解空间来寻找问题的解决方案。这种算法的效率通常受到问题规模和选择的数量的影响，因此在设计算法时需要注意选择的顺序和剪枝策略，以减少搜索空间，提高效率。

求解的代码如下：

import copy

def solve_sudoku(board):
    # 检查当前位置是否可填数字
    def is_valid(board, row, col, num):
        # 检查行是否合法
        for i in range(9):
            if board[row][i] == num:
                return False

        # 检查列是否合法
        for i in range(9):
            if board[i][col] == num:
                return False

        # 检查小九宫格是否合法
        start_row = 3 * (row // 3)
        start_col = 3 * (col // 3)
        for i in range(3):
            for j in range(3):
                if board[start_row + i][start_col + j] == num:
                    return False

        return True

    # 寻找下一个待填数字的位置
    def find_empty(board):
        for i in range(9):
            for j in range(9):
                if board[i][j] == 0:
                    return i, j
        return None

    # 递归解决数独
    def solve(board):
        # 找到下一个待填数字的位置
        find = find_empty(board)
        if not find:
            return True
        else:
            row, col = find

        # 尝试填入数字
        for num in range(1, 10):
            if is_valid(board, row, col, num):
                board[row][col] = num

                # 递归尝试填下一个位置
                if solve(board):
                    return True

                # 如果无解，回溯到上一个位置
                board[row][col] = 0

        return False

    # 创建数独副本，并进行求解
    board_copy = copy.deepcopy(board)
    if solve(board_copy):
        return board_copy
    else:
        return None

模拟鼠标键盘动作自动补全数独

import time
import pyautogui

from puzzle_getter import get_sudoku_board
from window_getter import get_window
from sudoku_solver import solve_sudoku

# 延迟运行画面捕捉，确保数独程序在最上层显示
# 当然也可以使用按键触发
print("Starting in 2s ...")
time.sleep(2)

print("Started.")
# 获取图像，生成numpy棋盘
image, (window_left, window_top) = get_window()
sudoku_board, top_left_pos, board_width = get_sudoku_board(image)
sudoku_board = list(sudoku_board)

# 求解数独
start_time = time.time()
solution = solve_sudoku(sudoku_board)
end_time = time.time()

if solution is not None:
    print("Used time : %.4fs"%(end_time-start_time))
    for row in solution:
        print(row)
else:
    print("No solution found.")

move_step = board_width // 9
base_position = (window_left + top_left_pos[0] + move_step // 2, window_top + top_left_pos[1] + move_step // 2)

# 设定每次操作间隔，单位s
pyautogui.PAUSE = 0.0015

for j in range(9):
    for i in range(9):
        if sudoku_board[j][i] != 0:
            continue
        pyautogui.click(base_position[0] + i * move_step, base_position[1] + j * move_step)
        # time.sleep(0.001)
        pyautogui.press(str(solution[j][i]))